码字和码距

在介绍汉明码之前，我们先简单回顾一下码字和码距的概念。不妨考虑最为经典的 ASCII 编码，我们可以用一个 8 位二进制数表示一个字符，例如 01100100 表示字符 d，01101101 表示字符 m，以此类推。每组 8 位二进制数便是该空间中的一个码字。同时，我们可以定义这个空间中的距离为两个码字不同的比特数，例如 01100100 和 01101101 的距离为 2。这一距离称汉明距离、码距。

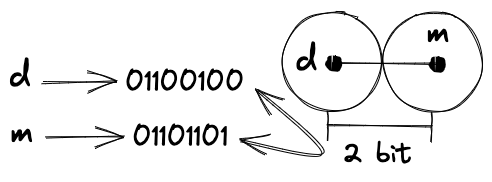
可以看到，可显示字符中任意两个码字的距离最小为 1。一旦传输中任意一个比特出错，便会对应到另一个码字，这对于通信的可靠性便提出了要求。人们需要一种方式给码字添加冗余信息，使得任意两个码字的距离至少为 2，以检测出传输中的错误。显然这里不是编码引论的教材，我不会详细介绍各类编码方案，只会简单介绍汉明码。

汉明码

汉明码是 1950 年由理查德·卫斯理·汉明提出的一种分组纠错码，其特点是任意两个码字的距离至少为 3。其思路是在编码时添加若干个冗余的奇偶校验位，以检测并纠正 1 比特的错误。其编码方式如下：

表中信息码字一行表示经汉明编码后的码字各位；来源一行表示码字的原始值是数据（Dx）还是校验位（Px）；校验位各行表示其是对哪些位进行奇偶校验的。

汉明码的这一编码方式对原始数据的长度没有任何限制，上表可以不断延伸以满足需求。不过一般编码时出于分析方便会讨论特定长度（）以简化情况。下面我会分别以(7, 4)汉明码和(11, 7)汉明码为例介绍汉明码。

(7, 4)汉明码

(7, 4)汉明码是指编码后的码字长度为 7，原始数据长度为 4 的汉明码。其编码方式如下：

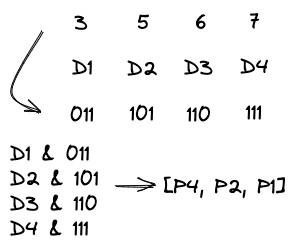
可以看到，对于原始数据的每个比特，先和其在信息码字中的位置的二进制表示进行与操作，再一齐进行异或操作，便得到了校验位的值。

这里以数据1001为例来演示一下编码和纠错。根据上述过程，我们可以写出校验位[P4 P2 P1] = 011 ^ 111 = 100，所以编码结果为0011001。假定传输中出现错误变为0011101，这时类似编码的计算校验位[P4 P2 P1] = 011 ^ 100 ^ 101 ^ 111 = 101，即第 5 个比特出错，纠错结果为0011001。

我们也可以使用矩阵描述其编码方式：

这里我们可以记中间的矩阵为 （生成矩阵），编码过程即原始信息 左乘 得到码字 。

为找出并纠正接收码字 中的错误，我们可以通过递增的二进制数构造一个矩阵 （检验矩阵）：

易知， 和 在二元域上的乘法满足：

这意味着，如果 无错误，那么 。如果 中有且仅有一个错误，那么 的结果必然非 0，并可以表示为 。其中 为错误位置的二进制表示（误码图样），即 仅由一个标识错误位置的 1 和若干的 0 组成。那么此时 的结果就是错误位置的二进制表示，我们可以通过这个错误位置的索引来纠正错误。

(7, 4)汉明系统码

前面的这种编码方式中数据和校验位交叉出现，这种编码方式称为非系统码。我们也可以将数据和校验位分开，这种编码方式称为系统码。可以通过对 进行初等列变换得到系统码的生成矩阵：

同样对于 ，我们可以通过对 进行初等变换得到系统码的校验矩阵：

不过，改为系统码后， 的结果显然与非系统码时一致，即不是系统码的错误位置表示。事实上对于更一般的系统码，从伴随式不能确定的推出误码图样 。通常采用根据 出现的概率制作一张译码表，根据 的值从译码表中查找 再进行纠正。

更一般的，如果我们从狭义的汉明设计的编码方案扩充为广义的，纠错能力为 1 的线性分组码，那么便不局限于上述的 和 。我们仅需利用汉明码的校验矩阵特性，对于 (n, k) 码，将 n-k 位不同的二进制数排列为 的各列，便得到一个校验矩阵。再对其进行列变换得到 ，进而得到对应的系统码的生成矩阵 ，即一种编码方案。

(11, 7)汉明码

下面我们来看看更一般的汉明码，可用于非扩展 ASCII 编码的(11, 7)汉明码。首先，根据汉明码的经典编码方式，构造出生成矩阵和校验矩阵：

同样，我们可以通过初等变换得到系统码的形式：

一般的汉明码其实和(7, 4)汉明码的差别不大，除了分析信息熵和其他能力时多一点小小的困难。这不是这篇文章的重点，所以这就是本文的全部内容了。希望你觉得这篇文章有点用。如果你有任何疑问，欢迎在评论区留言。

参考

1. 曹雪虹 信息论与编码[M]. 第 3 版. 北京: 淸华大学出版社, 2016.